





The delicate art of “seam carving” involves using various computing methods to resize images, while still preserving the core of the viewing experience. By this, we refer to the technique’s usage of various “energy functions” to determine which pixels to remove during the resizing process (indeed, a similar technique can be employed for the purpose of image enlargement, but here we choose to focus solely on reduction). The objective is to remove the pixels which have the least impact on the image (the “unimportant” ones).
The classic recipe for seam carving is as follows:
Ingredients:
Procedure:
An assortment of energy function may be used in tandem with this technique. Indeed, experts report that to this day, no “perfect” energy function has been found. Rather, individual energy functions have their strengths, and some may work better than others in certain cases. In the case of this reading, however, we showcase a modified version of the classic convolution-based function demonstrated in this superb paper.
But before we talk about energy functions, let us speak of gradients. Those who study the noble art of image processing will agree that gradient domain filtering is a powerful technique with many applications. Gradients can be used to exert high-level control over images, as they showcase low-level image features but cause drastic visual effects when modified. As one might expect, then, energy functions that leverage gradients allow us advantages such as the preservation of strong contours (a necessary capability, as the human eye is very sensitive to edges, making slight distortions in this area quite noticeable), because, as mentioned above, gradient-filtered images display areas of low-level significance. The following energy function (employed throughout this reading) takes advantage of these qualities and is intended to remove, as much as possible, pixels that blend in with their surroundings:
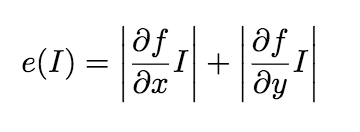
This particular energy function takes the partial derivative of an image’s pixels with respect to both the y and x axes, and takes the sum as the energy value. In this demonstration, we have modified the procedure slightly so as to:
Our final, modified energy function resembles the following:
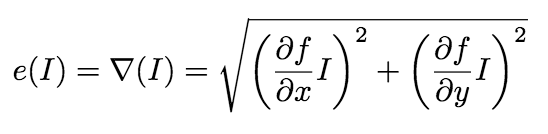

Original: 427x625

427x525

Original: 499x750

499x550

Original: 437x640

437x500

Original: 500x749

500x600

Original: 455x577

455x377

Original: 426x640

426x426

Original: 479x700 (Painting by Pascal Campion)

350x700

Original: 474x609

474x474

Original

400x400
The seam carving technique is noticeably flawed when dealing with images with defined lines or features. As such, photographs of people or distinct objects (cups, roads, houses) often become distorted after seam carving. Some examples of undesirable output are presented below. (Please note that images may have been resized to fit on the page. The actual, uncompressed dimensions of each image are listed on each image.)

Original: 564x552

564x400: The compression blatantly distorts the girl's face.

Original: 474x663

474x474: Distinctly shaped, man-made objects are usually oddly-shaped after carving.

Original: 500x678

450x550: Distinct edges are, more often than not, distorted. Notice that the foliage is relatively fine.
Seam carving seems to do best with images that involve seemingly random groups of pixels (often, these are nature images) that the human eye cannot easily distinguish between, or long stretches of “unimportant” information, such as blank space or darkness (the pumpkin image, above, is a good example of this). It is important, however, to note that often, artists include such blank stretches as elements of composition and movement. We thus find it somewhat regrettable that seam carving (through the demonstrated energy function) removes these features, which are intended to allow the viewer some amount of breathing room.
In fact, this brings up an interesting point about ethics. Should this technique ever be implemented in practice, it will likely only find success among publications and applications without an artistic application. It is not too farfetched to believe that those who find fulfillment in the production of creative visual works might take issue with their paintings and photographs being stretched and compressed without their consent. Piet Mondrian likely spent hours positioning his lines exactly the right distances from each other. Making it acceptable to modify these distances, changing them to the whim of viewers’ electronic devices, would likely have history’s virtuosos rolling in their graves.

Seam carving, with extra enhancements, can also be leveraged to remove certain objects from an image during reduction. One way to do this is to leverage a black and white mask (the image should only contain 1’s and 0’s), where the white areas resemble the shapes of objects you want removed during the compression process. The procedure is very similar to that of normal seam carving, except that after the energy function has been applied to the image (let’s call the result e(I) ), you’ll want to take the black and white mask (if it has three color channels, just extract one of the three to use) and subtract it from e(I). You can even multiply the mask by some constant to ensure the areas marked out in white are the number one priority for removal.

Original: 500x730 (Painting by Pascal Campion)

Mask: 500x730

400x730
This particular exampled worked very well because of the hazy forest background. Such randomness is less detectable and distinct to the human eye.
Of course, this technique is not perfect and sometimes the image will have noticeable seams where the object was removed, due to the photo having distinct objects in the background.

Original: 474x632

Mask: 474x632

350x632
Both the leaves and apples are immediately distinguishable to the viewer, which is why having the program remove a single apple and compress leads to unnatural-seeming lines and positions in the resulting image.
Through this experiment with seam carving, it’s clear that image processing is capable of incredible and truly surprising feats! I think image carving really demonstrates the relationship gradients have with edge strength, and that after this project, I feel like I understand its properties much better. I also think it worth noting that this project has taught me to never trust photography again and that despite its seemingly magical abilities, image processing is still incredibly imperfect.
Source Acknowledgements: Bell icon courtesy of Stanislav Levin. Title icons from left to right: Anbileru Adaleru, Gregory Sujkowski, Ludmil.